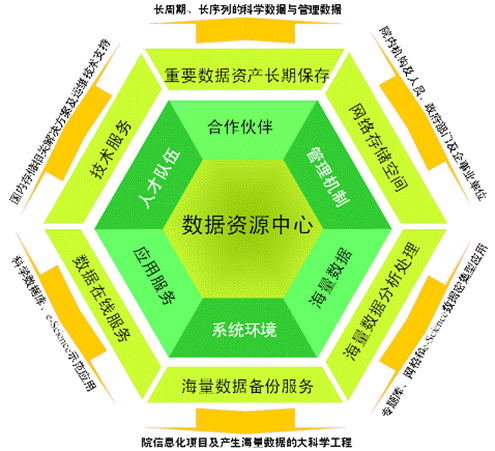
24考研数据结构核心考点精讲 图的邻接矩阵存储结构及其在数据处理与存储服务中的应用
在计算机考研(尤其是24考研)的数据结构科目中,图的存储结构是至关重要的核心章节。其中,邻接矩阵作为一种基础且直观的表示方法,不仅是笔试常考点,其思想也广泛应用于工业级的数据处理与存储服务中。本文将系统解析邻接矩阵的原理、特性,并探讨其在实际服务场景中的应用与考量。
一、邻接矩阵:图的数学化表示
邻接矩阵(Adjacency Matrix)是使用一个二维数组(矩阵)来表示图中顶点之间邻接关系的一种存储结构。
1. 定义与存储方法
对于一个具有 n 个顶点的图 G=(V, E),其邻接矩阵是一个 n × n 的方阵 A。矩阵中的元素 A[i][j] 定义如下:
- 对于无权图:如果顶点
i到顶点j之间存在边(或弧),则A[i][j] = 1;否则为0。 - 对于带权图(网络):如果顶点
i到顶点j之间存在边(或弧),则A[i][j] = 权值;否则通常用一个特定的值表示“无穷大”或“不存在”,如∞或一个非常大的数。
2. 代码表示(C语言风格)`c
#define MAXVERTEXNUM 100 // 最大顶点数
#define INFINITY 65535 // 用65535代表∞
typedef char VertexType; // 顶点数据类型
typedef int EdgeType; // 边权值类型
typedef struct {
VertexType vexs[MAXVERTEXNUM]; // 顶点表
EdgeType arcs[MAXVERTEXNUM][MAXVERTEXNUM]; // 邻接矩阵(边表)
int numVertexes, numEdges; // 图的当前顶点数和边数
} MGraph;`
3. 核心特性(考研重点)
- 空间复杂度:为 O(n²),与顶点数 n 的平方成正比,与边的数目 e 无关。因此,它更适用于存储稠密图(边数接近顶点数的平方)。
- 优点:
1. 直观性强:便于理解和实现。
- 查找效率高:可以快速判定任意两个顶点之间是否存在边,时间复杂度为
O(1)。
- 便于计算:方便计算顶点的度(在无向图中,第
i行或第i列的非零元素之和;在有向图中,出度为第i行之和,入度为第i列之和)。
- 缺点:
- 空间浪费:对于稀疏图,矩阵中大部分元素为0或∞,造成存储空间的大量浪费。
- 增删顶点不便:矩阵大小固定(静态数组实现时),动态增减顶点操作代价高。
二、邻接矩阵在数据处理与存储服务中的映射与应用
虽然在实际的大型分布式系统中,图数据通常使用邻接表、压缩稀疏矩阵或专门的图数据库(如Neo4j)来存储,但邻接矩阵的思想和变体依然在特定场景下发挥着关键作用。
1. 关系建模与快速查询服务
在中等规模或关系密集的系统中,邻接矩阵可以作为一个高效的“关系存在性查询”缓存。例如:
- 社交网络中的“是否关注”:将用户ID映射为矩阵索引,
A[i][j]=1表示用户i关注了用户j。虽然存储完整的海量用户矩阵不现实,但对于平台内的高频互动用户子集或关键KOL关系网,此结构能提供毫秒级的查询响应。 - 权限管理系统:快速验证“角色-资源”的访问权限。矩阵的行代表角色,列代表资源,值为1代表允许访问。
2. 图计算与机器学习的基础数据结构
许多图算法和机器学习模型的底层实现或数学表达依赖于矩阵运算。
- 推荐系统与图嵌入:用户-物品的交互关系可以构成一个二分图,其邻接矩阵是协同过滤等算法的基础输入。通过矩阵分解(如奇异值分解SVD)可以得到用户和物品的潜在特征向量。
- 路径计算与网络分析:在图论中,计算两点间长度为k的路径数目,恰好等于邻接矩阵A的k次幂
A^k中对应位置的值。这一性质被用于一些网络影响力分析或传播预测模型中。
3. 存储优化与实践考量
在实际的存储服务中,直接存储一个 n×n 的二维数组往往是低效的。因此产生了多种优化技术,这些思路本身也是高级数据结构的延伸:
- 稀疏矩阵压缩存储:对于稀疏图,采用三元组顺序表或十字链表等格式,只存储非零元素,从而大幅节约空间。这本质上是邻接矩阵思想与邻接表优点的结合。
- 分块与分布式存储:对于超大规模图,将大矩阵分块后分布式存储在不同的服务器节点上(例如基于Hadoop HDFS或Spark RDD),并行进行矩阵运算以完成图遍历或迭代计算。这是当前工业界处理海量图数据的主流范式之一。
- 位矩阵(Bit Matrix):对于最简单的无权图(仅表示关系是否存在),可以使用位图(Bitmap)来存储邻接矩阵,每个元素只占1个比特位,能将空间压缩到极致。例如,一个10万顶点的图,完整矩阵用位图存储约需
100000² / 8 ≈ 1.25 GB,虽然仍然很大,但相比整数存储已压缩了32倍。
三、考研视角下的
对于24考研学子而言,掌握邻接矩阵,不仅要会画图、会写代码定义、会分析时空复杂度,更要理解其应用场景的局限性(为何要引入邻接表等其他结构)和内在的数学本质(图与矩阵的深刻联系)。在解答算法设计题时,若题目隐含的图是稠密图,或需要频繁进行任意两点间的边存在性判断,那么选择邻接矩阵作为存储结构就是一个有力的论据。
将数据结构的理论知识与现代数据处理服务(如大数据、推荐系统)联系起来,能加深理解层次,这种跨领域的认知在复试面试中往往能展现出独特的优势。邻接矩阵从教科书中的一个经典结构,到分布式图计算中的分块矩阵,其核心思想一以贯之:用规范化的二维表格来抽象和量化实体间的复杂关联,这正是数据处理的精髓所在。
如若转载,请注明出处:http://www.aijiasichu.com/product/36.html
更新时间:2026-02-24 13:41:42